빅데이터 분석가 양성과정/Python - 머신러닝
차원축소(Unsupervised Learning)
황규진
2024. 7. 12. 15:24
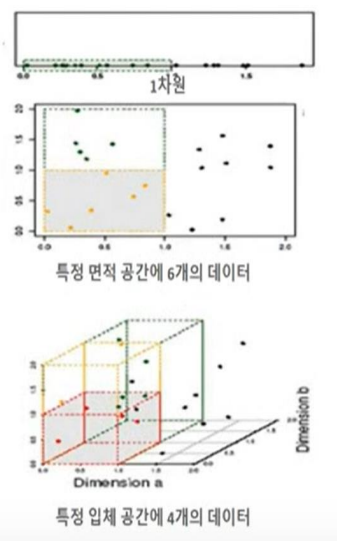
차원의 저주
차원이 커질수록
- 데이터 포인트들 간 거리가 크게 늘어남
- 데이터가 희소화 됨
- 수백~수천 개 이상의 피처로 구성된 포인트들 간 거리에 기반한 ML 알고리즘이 무력하됨
- 피처가 많을 경우 개별 피처간에 상관관계가 높아 선형 회귀와 같은 모델에서는 다중 공선성 문제로 모델의 예측 성능이 저하될 가능성이 높음
차원 축소의 장점
수십~수백개의 피처들을 작은 수의 피처들로 축소한다면?
- 학습 데이터 크기를 줄여서 학습 시간 절약
- 불필요한 피처들을 줄여서 모델 성능 향상
- 다차원 데이터를 3차원 이하의 차원 축소를 통해 시각적으로 보다 쉽게 데이터 패턴 인지
피처 선택과 피처 추출
피처 선택(feature selection)과 피처 추출(feature extraction)로 나눌 수 있습니다.
피처 선택
- 특정 피처에 종속성이 강한 불필요한 피처는 아예 제거하고, 데이터의 특징을 잘 나타내는 주요 피처만 선택
피처 추출
- 피처 추출은 기존 피처를 저차원의 중요 피처로 압축해서 추출. 새롭게 추출된 중요 특성은 기존 피처 반영해 압축된 것이지만 새로운 피처로 추출하는 것.

피처 추출
기존 피처를 단순 압축이 아닌, 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해 추출하는 것

차원 축소의 의미
단순히 데이터의 압축을 의미하는 것이 아닙니다. 더 중요한 의미는 차원 축소를 통해 좀 더 데이터를 잘 설명할 수 있는 잠재적 요소를 추출하는데 있습니다.
- 추천 엔진
- 이미지 분류 및 벼환
- 문서 토픽 모델링
PCA(Principal Component Analysis)
- 고차원의 원본 데이터를 저 차원의 부분 공간으로 투영하여 데이터 축소
- PCA는 원본 데이터가 가지는 데이터 변동성을 가장 중요한 정보로 간주하며 이 변동성에 기반한 원본 데이터 투영으로 차원 축소 수행
PCA 원리


- 제일 먼저 원본 데이터에 가장 큰 데이터 변동성을 기반으로 첫 번째 벡터 축 생성, 두 번째 축은 첫 번째 축을 제외하고 그 다음으로 변동성이 큰 축을 설정하는데 첫 번째 축에 직각이 되는 벡터(직교 벡터) 축 입니다.
- 세 번째 축은 다시 두 번째 축과 직각이 되는 벡터를 설정하는 방식으로 축을 생성
- 이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축의 개수 만큼의 차원으로 원본 데이터가 차원 축


- 즉 원본 데이터의 피처 개수에 비해 매우 작은 주 성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법
PCA 프로세스

공분산 행렬

선형 변환과 고유 벡터/고유값

공분산 행렬의 고유값 분해

PCA 요약
- PCA 변환
- 입력 데이터의 공분산 행렬이 고유 벡터와 고유 값으로 분해될 수 있으며, 이렇게 분해된 고유 벡터를 이용해 입력 데이터를 선형 변환하는 방식
- PCA 변환 수행 절차
- 입력 데이터 세트의 공분산 행렬을 생성
- 공분산 행렬의 고유벡터와 고유값을 계싼
- 고유값이 가장 큰 순으로 k개(PCA 변환 차수만큼)만큼 고유벡터 추출
- 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환
사이킷 런 PCA 클래스

- n_components 는 PCA 축의 개수 즉 변환 차원을 읨
- PCA 적용 전 입력 데이터의 개별 피처들 스케일링 해야함. 여러 속성을 PCA로 압축 전 각 피처들 값을 동일한 스케일로 변환 필요. 일반적으로 평균0, 분산 1인 표준 정규 분포로 변환. fit.transform으로 PCA 실행
- PCA 변환이 완료된 사이킷런 PCA 객체는 전체 변동성에서 개별 PCA 컴포넌트별로 차지하는 변동성 비율을 explained_variance_ratio_속성으로 제공
실습 - 붓꽃 데이터
데이터 읽어오기
from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# 사이킷런 내장 데이터 셋 API 호출
iris = load_iris()
# 넘파이 데이터 셋을 Pandas DataFrame으로 변환
columns = ['sepal_length','sepal_width','petal_length','petal_width']
irisDF = pd.DataFrame(iris.data , columns=columns)
irisDF['target']=iris.target
irisDF.head(3)

2 개의 속성(sepal_length, sepal_width)으로 타겟 산포도 시각화
#setosa는 세모, versicolor는 네모, virginica는 동그라미로 표현
markers=['^', 's', 'o']
#setosa의 target 값은 0, versicolor는 1, virginica는 2. 각 target 별로 다른 shape으로 scatter plot
for i, marker in enumerate(markers):
x_axis_data = irisDF[irisDF['target']==i]['sepal_length']
y_axis_data = irisDF[irisDF['target']==i]['sepal_width']
plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])
plt.legend()
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.show()

타겟 값들을 sepal_length, sepal_width 속성 변수들을 이용해서 2차원 평면에 뿌려봄
PCA 수행(n_components=2)
정규화(평균 0, 분산 1)
from sklearn.preprocessing import StandardScaler
# Target 값을 제외한 모든 속성 값을 StandardScaler를 이용하여 표준 정규 분포를 가지는 값들로 변환
iris_scaled = StandardScaler().fit_transform(irisDF.iloc[:, :-1])
PCA 수행(n_components=2)
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
#fit( )과 transform( ) 을 호출하여 PCA 변환 데이터 반환
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
print(iris_pca.shape)
2차원 PCA가 수행되었다
# PCA 환된 데이터의 컬럼명을 각각 pca_component_1, pca_component_2로 명명
pca_columns=['pca_component_1','pca_component_2']
irisDF_pca = pd.DataFrame(iris_pca, columns=pca_columns)
irisDF_pca['target']=iris.target
irisDF_pca.head(3)

PCA 차원 축소된 피처들로 데이터 산포도 시각화
#setosa를 세모, versicolor를 네모, virginica를 동그라미로 표시
markers=['^', 's', 'o']
#pca_component_1 을 x축, pc_component_2를 y축으로 scatter plot 수행.
for i, marker in enumerate(markers):
x_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_1']
y_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_2']
plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])
plt.legend()
plt.xlabel('pca_component_1')
plt.ylabel('pca_component_2')
plt.show()

- PCA(차원 축소) 이전에 비해 데이터들이 명확히 클러스터링된 것을 확인할 수 있다
print(pca.explained_variance_ratio_)
[0.72962445 0.22850762]
전체 변동성의 76%가 Component 1으로 설명될 수 있다
원본 데이터 vs PCA 데이터 간 예측성능 비교
원본 데이터와 PCA 변환된 데이터 간 랜덤포레스트 분류기 예측 성능 비
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import numpy as np
rcf = RandomForestClassifier(random_state=156)
scores = cross_val_score(rcf, iris.data, iris.target,scoring='accuracy',cv=3)
print('원본 데이터 교차 검증 개별 정확도:',scores)
print('원본 데이터 평균 정확도:', np.mean(scores))
원본 데이터 교차 검증 개별 정확도: [0.98 0.94 0.96]
원본 데이터 평균 정확도: 0.96
pca_X = irisDF_pca[['pca_component_1', 'pca_component_2']]
scores_pca = cross_val_score(rcf, pca_X, iris.target, scoring='accuracy', cv=3 )
print('PCA 변환 데이터 교차 검증 개별 정확도:',scores_pca)
print('PCA 변환 데이터 평균 정확도:', np.mean(scores_pca))

- PCA로 변환된 데이터가 원본 데이터보다 더 나은 예측 정확도를 보이는 것은 항상 그런 것은 아닙니다.
- PCA 변환 차원 개수에 따라 예측 성능이 떨어지기도 합니다.
- 4개의 속성이 2개의 속성이 되어도 예측 성능에 영향을 받지 않을 정도로 PCA 변환이 잘 되었음을 의미합니다.
- 다만, 고차원 데이터를 저차원으로 변환하면 직관적으로 이해하기 편하며, 데이터의 주축을 이루는 속성이 무엇인지 파악할 수 있습니다.