회귀의 개요
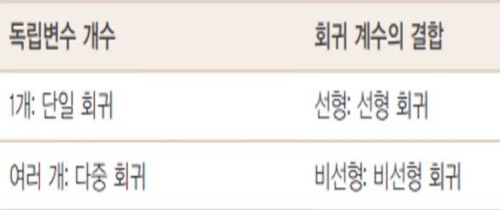
회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법
머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것입니다.
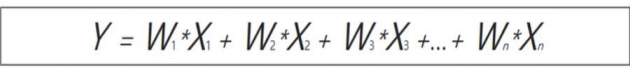
회귀의 유형
- 회귀 계수의 선형/비선형 여부, 돌립변수의 개수, 종속변수의 개수에 따라 여러가지 유형으로 나눌 수 있습니다.
- 회귀에서 가장 중요한 것은 바로 회귀 계수입니다. 이 회귀 계수가 ‘선형니냐 아니냐’ 에 따라 선형 회귀와 비선형 회귀로 나눌 수 있습니다.
- 그리고 독립변수의 개수가 한 개인지 여러 개인지에 따라 단인 회귀, 다중 회귀로 나뉩니다.
선형 회귀의 종류
- 일반 선형 회귀 : 예측 값과 실제 값의 RSS(Resicual Sum of Sauares)를 최소화 할 수 있도록 회귀 계수를 최적화 하며, 규제를 적용하지 않는 모델
- 릿지(Ridge) : 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델
- L2 - 영향을 제일 크게 미치는 것을 눌러줘서 영향을 줄인다.
- 라쏘(Lasso) : 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식
- L1 - 필요없는 것들 다 제거해준다.
- 엘라스틱넷(ElasticNet) : L2, L1 규제를 함께 결합한 모델
- 로지스틱 회귀(Logistic Regression) : 로지스틱 회귀는 사실 분류에 사용되는 선형 모델


RSS 기반의 회귀 오류 측정 -경사 하강법(Gradient Descent)
RSS
오류 값의 제곱을 구해서 더하는 방식. 미분 등의 계산을 편리하게 하기 위해서 RSS 방식으로 오류 합을 구합니다.

- RSS는 변수가 W0, W1인 식으로 표현할 수 있으며, 이 RSS를 최소로 하는 W0, W1, 즉 회귀 계수를 학습을 통해서 찾는 것이 머신러닝 기반 회귀 핵심 사항
- 회귀식의 독립변수 X, 종속변수 Y 가 중심 변수가 아니라 W 변수(회귀 계수)가 중심 변수 임을 인지하는 것이 매우 중요합니다.

- 회귀에서 이 RSS는 비용(Cost)이며 W 변수(회귀 계수) 로 구성되는 RSS를 비용 함수라고 합니다. 머신 러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값(즉, 오류 값)을 지속해서 감소시키고 최종적으로 더 이상 감소하지 않는 최소의 오류 값을 구하는 것입니다. 비용 함수를 손실함수 라고도 합니다.
비용 최소화 하기 - 경사 하강법(Gradient Descent)
W 파라미터의 개수가 많으면 고차원 방정식을 동원하더라고 해결 어렵다.
경사 하강법은 이런 문제 해결해 주면서 RSS 최소화 하는 방법을 직관적으로 볼 수 있다.

- 점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트 하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식
- 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정
- 오류 값이 더 이상 작아지지 않으면 그 오류 값을 최소 비용으로 판단하고 그떄의 W 값을 최적 파라미터로 반환
미분을 통해 비용 함수 최소 값
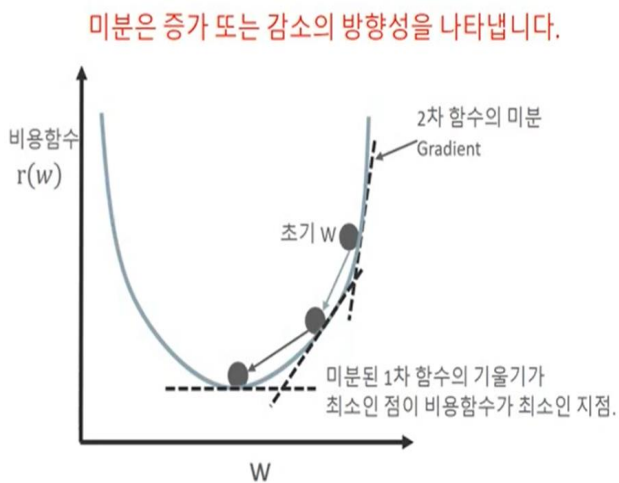
미분은 증가 또는 감소의 방향성을 나타냅니다.
비용함수가 다음 그림과 같은 포물선 형태 2차 함수라면 경사 하강법은 최초 W에서 미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 W를 업데이트 합니다.
마침내 더 이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그때의 W를 반환합니다.
RSS의 편미분
R(w)는 변수가 w 파라미터로 이뤄진 함수

R(w)를 미분해 미분 함수의 최솟값을 구해야 하는데,
R(w)는 두 개의 w 파라미터인 w0와 w1을 각각 가지고 있기 때문에 일반적인 미분을 적용 할 수 없고,
wo, w1 각 변수에 편미분을 적용해야 한다.
R(w)를 최소화 하는 w0와 w1의 값은 각각 R(w)를 w0, w1으로 순차적으로 편미분을 수행해 얻을 수 있습니다.





수행 프로세스
- step 1: w1, w0를 임의의 값으로 설정하고 첫 비용 함수의 값을 계산
- step 2 :

으로 업데이트 한 후 다시 비용 함수의 값 계산
- step 3 : 비용 함수의 값이 감소했으면 다시 step 2 반복, 감소 하지 않으면 그때의 w1, w0 구하고 반복 중지
경사하강법 ( Gradient Descent )
#실제값을 Y=4X+6 시뮬레이션하는 데이터 값 생성
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y = 4X + 6 식을 근사(w1=4, w0=6). random 값은 Noise를 위해 만듬
X = 2 * np.random.rand(100,1)
y = 6 +4 * X+ np.random.randn(100,1)
# X, y 데이터 셋 scatter plot으로 시각화
plt.scatter(X, y)

# w1 과 w0 를 업데이트 할 w1_update, w0_update를 반환.
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
# 먼저 w1_update, w0_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
# 예측 배열 계산하고 예측과 실제 값의 차이 계산
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
# w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
print(diff.shape)
w0_factors = np.ones((100,1))
w1_update = -(2/100)*0.01*(np.dot(X.T, diff))
w0_update = -(2/100)*0.01*(np.dot(w0_factors.T, diff))
print(w1_update.shape, w0_update.shape)
w1, w0
(100, 1)
(1, 1) (1, 1)
(array([[0.]]), array([[0.]]))
#반복적으로 경사 하강법을 이용하여 get_weigth_updates()를 호출하여 w1과 w0를 업데이트 하는 함수 생성
# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용함.
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화.
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
#예측 오차 비용을 계산을 수행하는 함수 생성 및 경사 하강법 수행
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
w1:4.022 w0:6.162
Gradient Descent Total Cost:0.9935
plt.scatter(X, y)
plt.plot(X,y_pred)

미니 배치 확률적 경사 하강법을 이용한 최적 비용함수 도출 - Stochastic Gradient Descent
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index =0
for ind in range(iters):
np.random.seed(ind)
# 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
w1: 4.028 w0: 6.156
Stochastic Gradient Descent Total Cost:0.9937
⇒ 둘 다 결과 값 비슷하지만 속도가 SGD(Stochastic Gradient Descent)가 훨씬 빠름. 그래서 SGD를 많이 사용, 딥러닝 에서는 Adam 많이 사용
Linear Regression

- LinearRegreesion 클래스는 예측값과 실제 값의 RSS를 최소화해 OLS 추정 방식으로 구현한 클래스
- fit()메서드로 X, y 배열을 입력 받으면 회귀 계수 인 W 를 coef_ 속성에 저장
선형 회귀의 다중 공선성 문제
- 일반적으로 선형 회귀는 입력 피처의 돌깁성에 많은 영향을 받습니다. 피처간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해 집니다. 이러한 현상을 다중 공선성 문제라고 합니다. 일반적으로 상관관계 가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용합니다.
회귀의 평가 지표

회귀 평가 API


'빅데이터 분석가 양성과정 > Python - 머신러닝' 카테고리의 다른 글
| 회귀(Regression) - 다항 선형 회귀 (0) | 2024.07.12 |
|---|---|
| 회귀(Regression) - 예제 (0) | 2024.07.12 |
| 실습) adult data 분류 (0) | 2024.07.11 |
| 머신러닝 분류 - 앙상블 러닝 (2) | 2024.07.11 |
| 머신러닝 분류 - 분류 알고리즘 ( 결정 트리 ) (2) | 2024.07.11 |
