함수
- 두 집합 사이의 관계를 설명하는 수학 개념
- 변수 x가 있을 때 x가 변하면 이에 따라 y는 어떤 규칙으로 변하는지 나타냄
일차함수 ( 기울기와 절편 )
- 일차 함수 : y가 x에 관한 1차식으로 표현된 함수를 말함
- ex ) $y = ax + b , ( a ≠ 0 )$

실습 코드
# 1차 함수
# 1차 함수, 𝒚=𝒂𝒙+𝒃 (𝒂≠𝟎)에서 𝒂=𝟏, 𝒃=𝟐일 때 𝒚의 그래프를 그리시오
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, 4, 100)
a = 1
b = 2
y = a * x + b
plt.plot(x,y)
plt.grid()
plt.title('$f(x)=x+2$')
plt.show()

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, 4, 100)
a = 1
b = 2
y = a*x + b
plt.plot(x,y)
plt.xlabel('x') # x label 추가
plt.ylabel('y') # y label 추가
plt.title('$y=ax+b$') # 타이틀에 수식 넣기
plt.axhline(0,color='black') # 수평 좌표선 (y=0)
plt.axvline(0,color='black') # 수직 좌표선 (x=0)
plt.grid()
plt.show()

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, 4, 100)
a = 1
b = 2
y = a*x + b
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('$y={}x+{}$'.format(a, b)) # 타이틀에 수식 넣기
plt.axhline(0,color='black')
plt.axvline(0,color='black')
plt.grid()
plt.show()

입출력 관계를 그래프로 그리시오.

import matplotlib.pyplot as plt
X = [0, 2, 4, 6, 8]
y = [0, 4, 8, 12, 16]
plt.plot(X, y, marker='s')
plt.grid()
plt.show()

공부한 시간 대비 취득 성적을 그래프로 나타내시오.

import matplotlib.pyplot as plt
hour = [2, 4, 6, 8]
jumsu = [81, 93, 91, 97]
plt.plot(hour, jumsu, marker='s')
plt.grid()
plt.xlabel('Hour')
plt.ylabel('Jumsu')
plt.show()
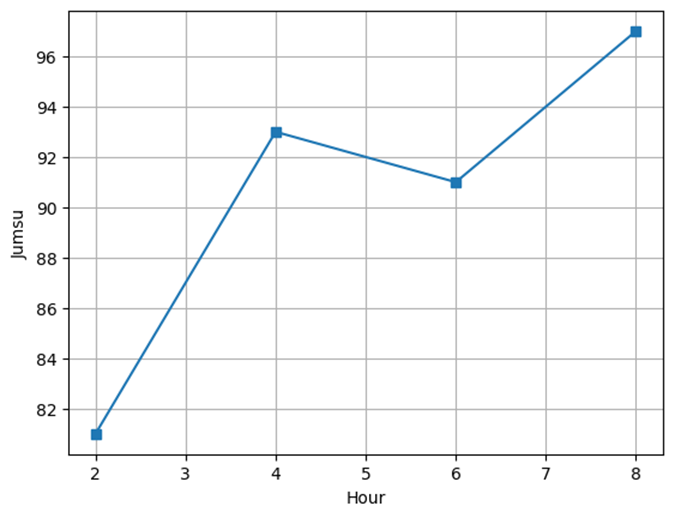
1차 함수(진선 그래프)로 근사화
import matplotlib.pyplot as plt
import numpy as np
hour = [2, 4, 6, 8]
jumsu = [81, 93, 91, 97]
plt.plot(hour, jumsu, marker='s')
plt.grid()
plt.xlabel('Hour')
plt.ylabel('Jumsu')
a = 2
b = 81
x = np.array(hour)
y = a*x + b
plt.plot(x,y, marker='o')
plt.show()

이차함수와 최솟값
- 이차함수 : y가 x에 관한 2차식으로 표현된 함수를 말함


실습 코드
여기서 a 가 양수일 때 임의의 2차 함수 그래프를 그리시오

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-6, 6, 64)
y = x**2
plt.plot(x, y)
plt.grid()
plt.show()

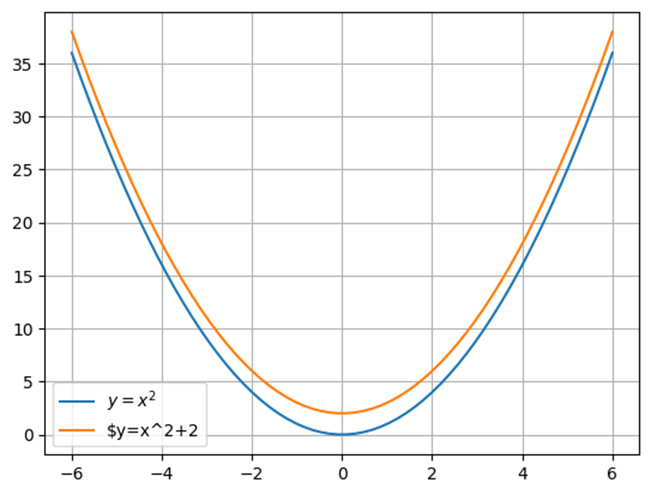
여기서 a 가 양수 1 이다. q가 0과 2일때의 함수 그래프를 그리시오

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-6, 6, 64)
q = 2
y0 = x**2
y1 = x**2 + q
plt.plot(x, y0, label='$y=x^2$')
plt.plot(x, y1, label='$y=x^2+2')
plt.legend()
plt.grid()
plt.show()
a 가 양수 1 이고 q가 10이다. p값이 0,1,2일 때의 함수 그래프를 그리시오

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-6, 8, 64)
a = 1
q = 10
#y = [ a*(x-p)**2 + q for p in range(3)]
y = []
for p in range(3):
y.append( a*(x-p)**2 + q)
for i, yn in enumerate(y):
plt.plot(x, yn, label=f'$p={i}$')
plt.title('$y=(x-p)^2 + 10$')
plt.legend()
plt.grid()
plt.show()


a = 1;p = 1;q = 3
x = np.linspace(-4,8, 100)
y = a*(x-p)**2 + q
plt.figure(figsize=(4,4)) # 그림 크기 지정
plt.plot(x, y)
plt.plot(p, q, 's')
plt.text(p,q, '({},{})'.format(p, q))
plt.axhline(0,color='black')
plt.axvline(0,color='black')
plt.grid()
plt.show()



미분, 순간 변화율과 기울기
- 미분은 순간 변화율을 구하는 것이다.





편미분
- 독립 변수가 1개인 경우 미분하라고 하면 그 독립 변수가 순간 변화값 대비 출력 변화를 구하는 것이 ‘미분’이다.
- 특정 독립 변수를 관심 변수로 두고 나머지(N-1) 개의 변수는 고정된 값(상수)로 간주하고 미분을 진행하는 것 =편미분

지수와 지수함수


코드 실습
x = np.linspace(-4,4, 100)
plt.subplot(1, 2, 1)
a = 2
y = a**x
plt.plot(x, y)
plt.axhline(0,color='black')
plt.axvline(0,color='black')
plt.grid()
plt.title('$y=a^x$ (a > 1)')
plt.subplot(1, 2, 2)
a = 0.5
y = a**x
plt.plot(x, y)
plt.axhline(0,color='black')
plt.axvline(0,color='black')
plt.grid()
plt.title('$y=a^x$ (0 < a < 1)')
plt.show()

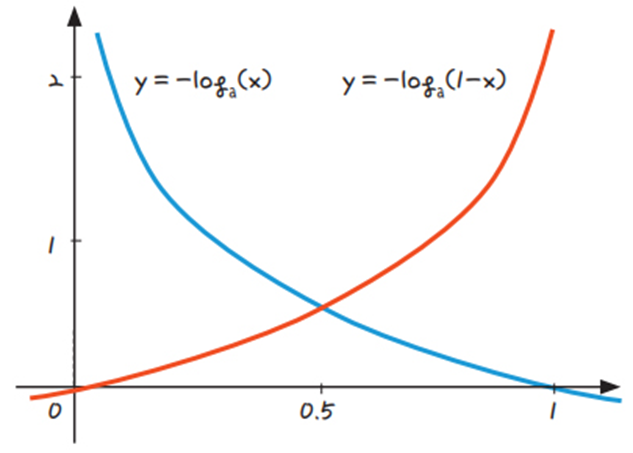
로그와 로그함수


실습 코드

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.0001, 0.9999, 128)
y0 = - np.log10(x)
y1 = - np.log10(1 - x)
plt.plot(x,y0)
plt.plot(x,y1)
plt.grid()
plt.show()
가중합

- 가중합


시그모이드 함수


실습 코드
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-8, 8, 64)
y = 1 / ( 1+np.exp(-x))
plt.plot(x, y)
plt.title('sigmoid')
plt.grid()
plt.show()

로지스틱 회귀 분석


import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(65, 95, 64)
d = (81+72/2)
y = 1 / ( 1 + np.exp(-(x-d)))
plt.grid()
plt.plot(x, y)
plt.title('sigmoid')
plt.xlabel('$x$')
plt.xlim(min(x), max(x))
plt.show()

경사도
import numpy as np
import matplotlib.pyplot as plt
y = []
x = np. linspace(-5, 5, 128)
a_lst = range(1, 11, 2)
for a in a_lst:
y.append( 1 / (1 + np.exp(-a*x)) )
for idx in range(0, len(a_lst)):
plt.plot(x, y[idx], label=f' $a={a_lst[idx]}$')
plt.title(r'$#frac{1}{ 1+e^{-(ax)} }$')
plt.xlabel('$x$')
plt.xticks(np.arange(-5, 6))
plt.xlim([min(x), max(x)])
plt.legend()
plt.grid()
plt.show()

- 시그모이드 함수에서 a값이 작아지면 오차는 커짐
- 시그모이드 함수에서 a값이 커지면 오차는 작아짐
import numpy as np
import matplotlib.pyplot as plt
y = []
x = np. linspace(-5, 5, 128)
C = 3
a = C
b_lst = range(0, 10, 2)
for a in a_lst:
y.append( 1 / (1 + np.exp(-(a * x + b))))
for idx in range(0, len(b_lst)):
plt.plot(x, y[idx], label=f' $b={b_lst[idx]}$')
plt.title(r'$#frac{1}{ 1+e^{-(3x+b)}}$')
plt.xlabel('$x$')
plt.xticks(np.arange(-5, 6))
plt.xlim([min(x), max(x)])
plt.legend(loc = 4)
plt.grid()
plt.show()

- 시그모이드 함수에서 b값이 작아지면 오차는 커짐
- 시그모이드 함수에서 b값이 커지면 오차는 커짐

- P는 예측값
P = np.linspace(0.001,1,128)
y = -np.log2(P)
plt.plot(P,y, 'r')
plt.xlim([0,1])
plt.xlabel('$P$')
plt.title('$-log_2{P}$')
plt.yticks(np.arange(0, 14))
plt.grid()
plt.show()


P = np.linspace(0.001, 0.999, 128)
y = -np.log2(1-P)
plt.plot(P,y, 'r')
plt.xlim([0,1])
plt.xlabel('$P$')
plt.title('$-log_2{(1-P)}$')
plt.xticks(np.arange(0, 1.1, 0.1))
plt.grid()
plt.show()


import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.0001, 0.9999, 128)
y0 = - np.log10(x)
y1 = - np.log10(1 - x)
plt.plot(x,y0)
plt.plot(x,y1)
plt.grid()
plt.show()

ReLU 함수
import numpy as np
import matplotlib.pyplot as plt
def softmax(x):
return np.exp(x)/np.sum(np.exp(x))
x = np.array([2, 3, 4, 1])
y = softmax(x)
print(y)
print(sum(y))
[0.08714432 0.23688282 0.64391426 0.0320586 ]
1.0
tanh 함수
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = 2/( 1+np.exp(-2*x) ) - 1
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('$y = 2/(1+e^{-x}) - 1$')
plt.grid()
plt.show()

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = np.tanh(x)
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('$y = tanh(x)$')
plt.grid()
plt.show()

'빅데이터 분석가 양성과정 > Python - 딥러닝' 카테고리의 다른 글
| 오류역전파 (0) | 2024.07.17 |
|---|---|
| 퍼셉트론(XOR) (0) | 2024.07.17 |
| 로지스틱 회귀 (0) | 2024.07.17 |
| 선형회귀 (0) | 2024.07.17 |
| 개요 (0) | 2024.07.17 |
