규제 선형 회귀(릿지, 라쏘, 엘라스틱넷)
과대 적합을 방지하기 위해서 규제는 필요하다.
회귀 모델은 적절히 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어할 수 있어야 합니다.
최초 목표는 RSS(오차)를 최소화 하는 것이었지만, 그러다보니 회귀 계수가 커져서 과대적합이라는 문제를 만나게 되었다.
그래서 RSS와 더불어 회귀 계수 크기를 밸런스 있게 제어하는 것이 필요하게 되었다.
→ 비용 함수의 목표가 밸런스 조절(RSS값 최소화, 회계 계수 값 제어)이 됨
알파값으로 비용 함수의 회귀 계수 조절
- 비용함수에 alpha 값으로 페널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 규제라고 부릅니다.
- 규제는 크게 L2 방식과 L1 방식으로 구분됩니다.
- L2규제는 위에서 설명한 바와 같이 w의 제곱에 대해 페널티를 부여하는 방식을 말합니다. L2 규제를 적용한 회귀를 릿지(Ridge)회귀라고 합니다.
- 라쏘(Lasso)회귀는 L1규제를 적용한 회귀 입니다. L1규제는 w의 절댓값에 대해 페널티를 부여합니다. L1 규제를 적용하면 영향력이 크지 않은 회귀 계수 값을 0으로 변환합니다.
- ElasticNet : L2, L1규제를 함께 결합한 모델입니다. 주로 피처가 많은 데이터 세트에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정합니다.
릿지 회귀
보스턴 집값 예측
# 앞의 LinearRegression예제에서 분할한 feature 데이터 셋인 X_data과 Target 데이터 셋인 Y_target 데이터셋을 그대로 이용
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
# boston 데이타셋 로드
boston = load_boston()
# boston 데이타셋 DataFrame 변환
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)
# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함.
bostonDF['PRICE'] = boston.target
print('Boston 데이타셋 크기 :',bostonDF.shape)
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
ridge = Ridge(alpha = 10)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 3))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores,3))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))
Boston 데이타셋 크기 : (506, 14)
5 folds 의 개별 Negative MSE scores: [-11.422 -24.294 -28.144 -74.599 -28.517]
5 folds 의 개별 RMSE scores : [3.38 4.929 5.305 8.637 5.34 ]
5 folds 의 평균 RMSE : 5.518
- 규제를 적용하지 않은 선형 회귀는 RMSE가 5.829였으므로 모델 성능이 향상된 것을 확인할 수 있다
alpha값을 0 , 0.1 , 1 , 10 , 100 으로 변경하면서 RMSE 측정
# Ridge에 사용될 alpha 파라미터의 값들을 정의
alphas = [0 , 0.1 , 1 , 10 , 100]
# alphas list 값을 iteration하면서 alpha에 따른 평균 rmse 구함.
for alpha in alphas :
ridge = Ridge(alpha = alpha)
#cross_val_score를 이용하여 5 fold의 평균 RMSE 계산
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0} 일 때 5 folds 의 평균 RMSE : {1:.3f} '.format(alpha,avg_rmse))
alpha 0 일 때 5 folds 의 평균 RMSE : 5.829
alpha 0.1 일 때 5 folds 의 평균 RMSE : 5.788
alpha 1 일 때 5 folds 의 평균 RMSE : 5.653
alpha 10 일 때 5 folds 의 평균 RMSE : 5.518
alpha 100 일 때 5 folds 의 평균 RMSE : 5.330
- 알파값이 증가할수록 모델 성능이 향상되고 있다
알파 값이 증가할수록 실제로 회귀 계수 값이 작아지는지 확인해보기
# 각 alpha에 따른 회귀 계수 값을 시각화하기 위해 5개의 열로 된 맷플롯립 축 생성
fig , axs = plt.subplots(figsize=(18,6) , nrows=1 , ncols=5)
# 각 alpha에 따른 회귀 계수 값을 데이터로 저장하기 위한 DataFrame 생성
coeff_df = pd.DataFrame()
# alphas 리스트 값을 차례로 입력해 회귀 계수 값 시각화 및 데이터 저장. pos는 axis의 위치 지정
for pos , alpha in enumerate(alphas) :
ridge = Ridge(alpha = alpha)
ridge.fit(X_data , y_target)
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=ridge.coef_ , index=X_data.columns )
colname='alpha:'+str(alpha)
coeff_df[colname] = coeff
# 막대 그래프로 각 alpha 값에서의 회귀 계수를 시각화. 회귀 계수값이 높은 순으로 표현
coeff = coeff.sort_values(ascending=False)
axs[pos].set_title(colname)
axs[pos].set_xlim(-3,6)
sns.barplot(x=coeff.values , y=coeff.index, ax=axs[pos])
# for 문 바깥에서 맷플롯립의 show 호출 및 alpha에 따른 피처별 회귀 계수를 DataFrame으로 표시
plt.show()
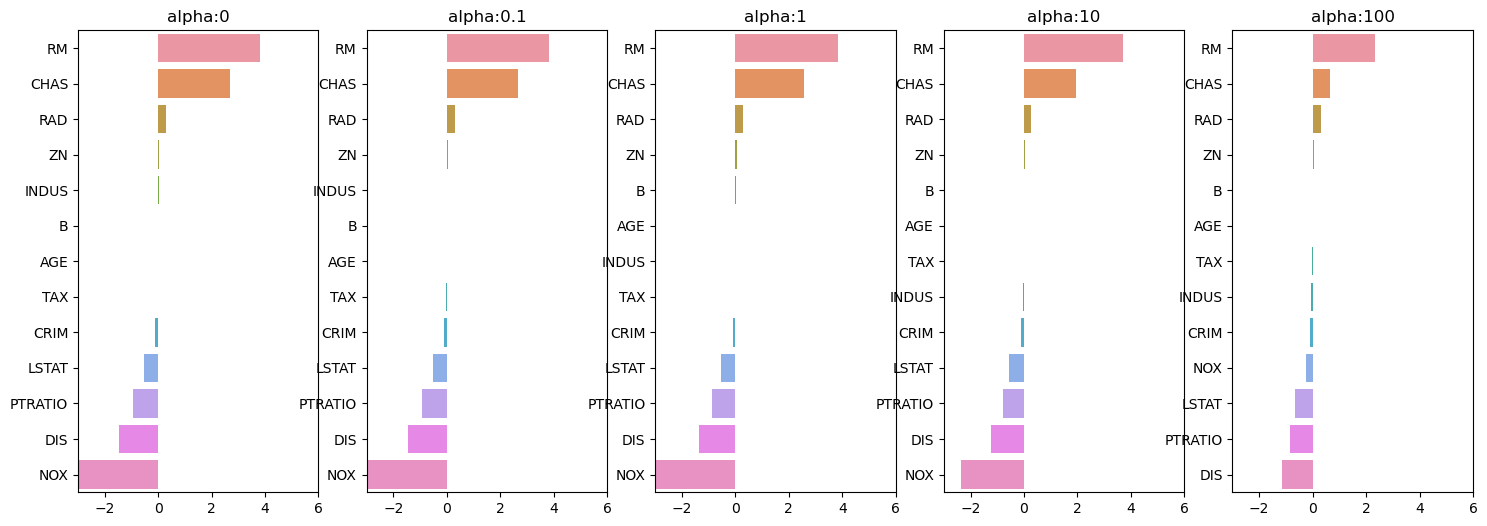
NOX가 많이 작아져서 다른 회귀 계수와 스케일이 비슷해짐
ridge_alphas = [0 , 0.1 , 1 , 10 , 100]
sort_column = 'alpha:'+str(ridge_alphas[0])
coeff_df.sort_values(by=sort_column, ascending=False)
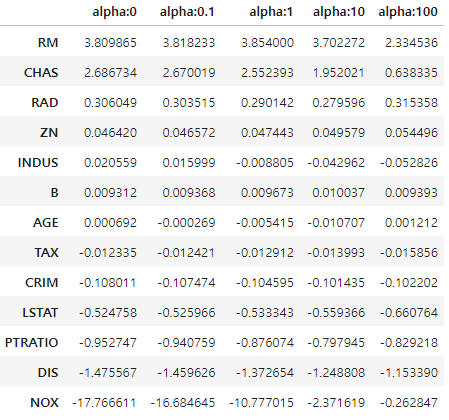
- 릿지 회귀에서 알파값이 증가할수록 NOX값의 감소하여서 다른 회귀 계수 값들과 스케일이 비슷해졌다. 이로 인해 기존 회귀 모델의 성능이 개선되었다.
라쏘 회귀
L2 규제가 회귀 계수의 크기를 감소시키는 데 반해, L1 규제는 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거합니다.
L2 규제 vs L1 규제
- L2의 경우에는 가중치의 값을 이용합니다. 어느 정도 튀는 값에 대해 대응할 수 있다는 소리죠. 따라서, 이상치나 노이즈가 있는 데이터에 대한 학습을 진행할 때 사용하면 좋습니다. 특히 선형 모델의 일반화에 좋습니다.
- →L2규제는 회귀 계수 값의 증감을 관리한다.
- L1의 경우에는 가중치의 크기에 상관없이 상수값을 뺍니다. 이는 대체적으로 불필요한 가중치의 수치를 0으로 만들도록 하는 방향으로 적용됩니다. 즉, 중요한 가중치만을 취하기 때문에 sparse feature에 대한 모델을 구성하는데 적합합니다.
- → L1규제는 회귀에 적절한 피처만 포함시키는 피처 셀렉션의 특성을 가진다
평균 RMSE, 회귀 계수 값들을 반환해주는 함수 이용
from sklearn.linear_model import Lasso, ElasticNet
# alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None,
verbose=True, return_coeff=True):
coeff_df = pd.DataFrame()
if verbose : print('####### ', model_name , '#######')
for param in params:
if model_name =='Ridge': model = Ridge(alpha=param)
elif model_name =='Lasso': model = Lasso(alpha=param)
elif model_name =='ElasticNet': model = ElasticNet(alpha=param, l1_ratio=0.7)
neg_mse_scores = cross_val_score(model, X_data_n,
y_target_n, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} '.format(param, avg_rmse))
# cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출
model.fit(X_data_n , y_target_n)
if return_coeff:
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=model.coef_ , index=X_data_n.columns )
colname='alpha:'+str(param)
coeff_df[colname] = coeff
return coeff_df
# end of get_linear_regre_eval
# 라쏘에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
lasso_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_lasso_df =get_linear_reg_eval('Lasso', params=lasso_alphas, X_data_n=X_data, y_target_n=y_target)
####### Lasso #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.612
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.615
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.669
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.776
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.189
알파값이 0.07일 때 RMSE가 가장 좋다
print(lasso_alphas)
[0.07, 0.1, 0.5, 1, 3]
라쏘는 알파 값이 증가되면 특정 피처의 회귀 계수를 0으로 만들어서 해당 피처를 회귀식에서 제외시켜 버린다
# 반환된 coeff_lasso_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(lasso_alphas[0])
coeff_lasso_df.sort_values(by=sort_column, ascending=False)
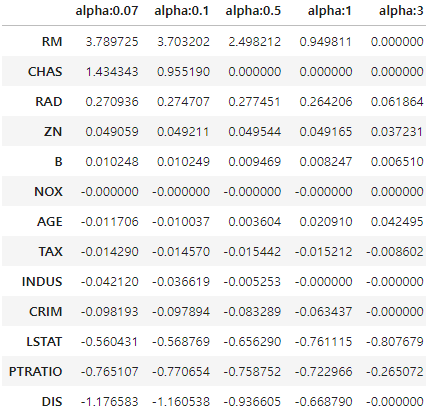
알파값 0.5 이상일 때 CHAS 회귀 계수 값을 0으로 만들어 버림
알파값 0.07 부터 NOX 회귀 계수 값을 0으로 만들어 버림
엘라스틱넷 회귀
- 엘라스틱넷 회귀는 L2 규제와 L1 규제를 결합한 회귀입니다. 따라서 엘라스틱넷 회귀 비용함수의 목표는 최소화 하는 w를 찾는 것입니다.
- 엘라스틱넷은 라쏘 회귀가 서로 상관관계가 높은 피처들의 경우에 이들 중에서 중요 피처만을 셀렉션 하고 다른 피처들은 모두 회귀 계수를 0으로 만드는 성향이 강합니다. 특히 이러한 성향으로 인해 alpha 값에 따라 회귀 계수의 값이 급격히 변동할 수도 있는데, 엘라스틱넷 회귀는 이를 완화하기 위해 L2 규제를 라쏘 회귀에 추가한 것입니다.
- 엘라스틱넷 클래스의 주요 생성 파라미터는 alpha 와 l1_ratio 입니다.
- 엘라스틱넷의 규제는 a L1 규제 + b L2 규제로 정의될 수 있습니다.



# 엘라스틱넷에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
# l1_ratio는 0.7로 고정
elastic_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_elastic_df =get_linear_reg_eval('ElasticNet', params=elastic_alphas,
X_data_n=X_data, y_target_n=y_target)
####### ElasticNet #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.542
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.526
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.467
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.597
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.068
알파값이 0.5일 때 RMSE가 가장 좋다
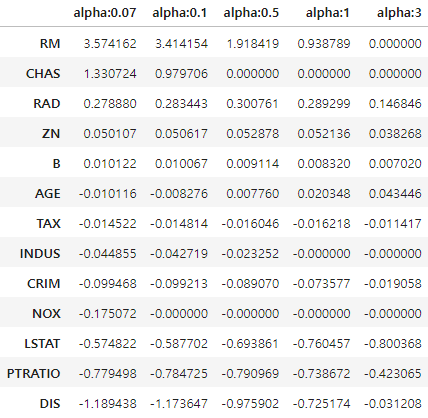
# 반환된 coeff_elastic_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(elastic_alphas[0])
coeff_elastic_df.sort_values(by=sort_column, ascending=False)
'빅데이터 분석가 양성과정 > Python - 머신러닝' 카테고리의 다른 글
| 회귀(Regression) - 로지스틱 회귀 / 회귀 트리 (0) | 2024.07.12 |
|---|---|
| 회귀(Regression) - 데이터 전처리(정규화, 로그 변환, 스케일러, 원-핫 인코딩) (0) | 2024.07.12 |
| 회귀(Regression) - 다항 선형 회귀 (0) | 2024.07.12 |
| 회귀(Regression) - 예제 (0) | 2024.07.12 |
| 회귀(Regression) - 선형 회귀 / 경사 하강법 (0) | 2024.07.12 |
