💡탐색적 데이터 분석 (데이터 이해와 시각화 기법 추가)
- 데이터의 출처와 주제에 대해 이해
- 데이터의 크기 확인
- 데이터 구성 요소(feature)의 속성(특징) 확인
feature 의 데이터를 어떻게 더 깊게 이해할 수 있을까?
1. 데이터 분석을 위한 위치 추정과 범위 추정
탐색적 데이터 분석의 세 번째, feature 분석을 위한 기본 탐색
- 위치 추정: 방대한 데이터의 대푯값을 구해서, 해당 feature의 일종의 요약 정보 도출
- 보통은 평균을 쓰면 되며(물론 평균이 가장 좋은 대푯값이 아닌 경우도 많음), 특정 튀는 수치가 있을 때만 조정해도 충분합니다!
- 변이 추정: 방대한 데이터의 분포 (밀집해 있는지, 퍼져 있는지)를 알아내어, 역시 해당 feature의 일종의 요약 정보 도출
- 수학에서 익힌 표준편차, 분산가 대표적인 분포 확인 값
위치 추정
- feature를 대표할 수 있는 대푯값을 찾는 것
평균 (mean)
- 모든 값을 갯수로 나눈 값
가중 평균 (weighted mean)
- 데이터 값 X 가중치의 총합을 다시 가중치의 총합으로 나눈 것
- 예: 여러 기기로부터 가져온 데이터 중, 특정 기기는 신뢰도가 떨어질 경우, 해당 기기로부터 나온 데이터에는 가중치를 낮게 줌
중간값 (median) (가중 중간값도 가능)
- 데이터를 정렬한 후 중간에 위치한 값을 취함
- 평균은 특잇값(outlier)에 큰 영향을 받으므로, 특잇값에 큰 영향을 받지 않도록 중간값을 활용할 수 있음
절사평균 (trimmed mean)
- 데이터를 정렬한 후, 양끝에서 일정 개수의 값들을 빼고, 남은 데이터를 기반으로 평균을 계산
- 즉, 특잇값을 평균을 구할 때 제외하는 것임
EDA 에서는 중간값(또는 중앙값 이라고도 불리움)을 평균보다 중요하게 사용
변이 추정
분산(variance)
- 평균과 각 데이터간의 차를 제곱한 값들의 합을 데이터 갯수로 나눈 값
- σ2 : 모분산 (깊게 들어가면 샘플 분산은 n - 1 로 나누지만, 분산의 형태만 간략히 참고로 알아두기로 함)
- μ : 평균
- N : 데이터 갯수
- xi : i 번째 데이터
표준편차(standard deviation)
- 분산은 수치가 너무 커서, 분산의 제곱근 (루트를 씌운 값)
- σ : 모 표준편차 (깊게 들어가면 샘플 표준편차는 샘플 분산이 n 이 아닌, n - 1 로 나눈 값이므로 이를 제곱근한 값)
import pandas as pd
df = pd.DataFrame({
'A': [1, 2, 3, 4, 5, 6],
'C': [1, 2, 3, 4, 5, 100]
})
df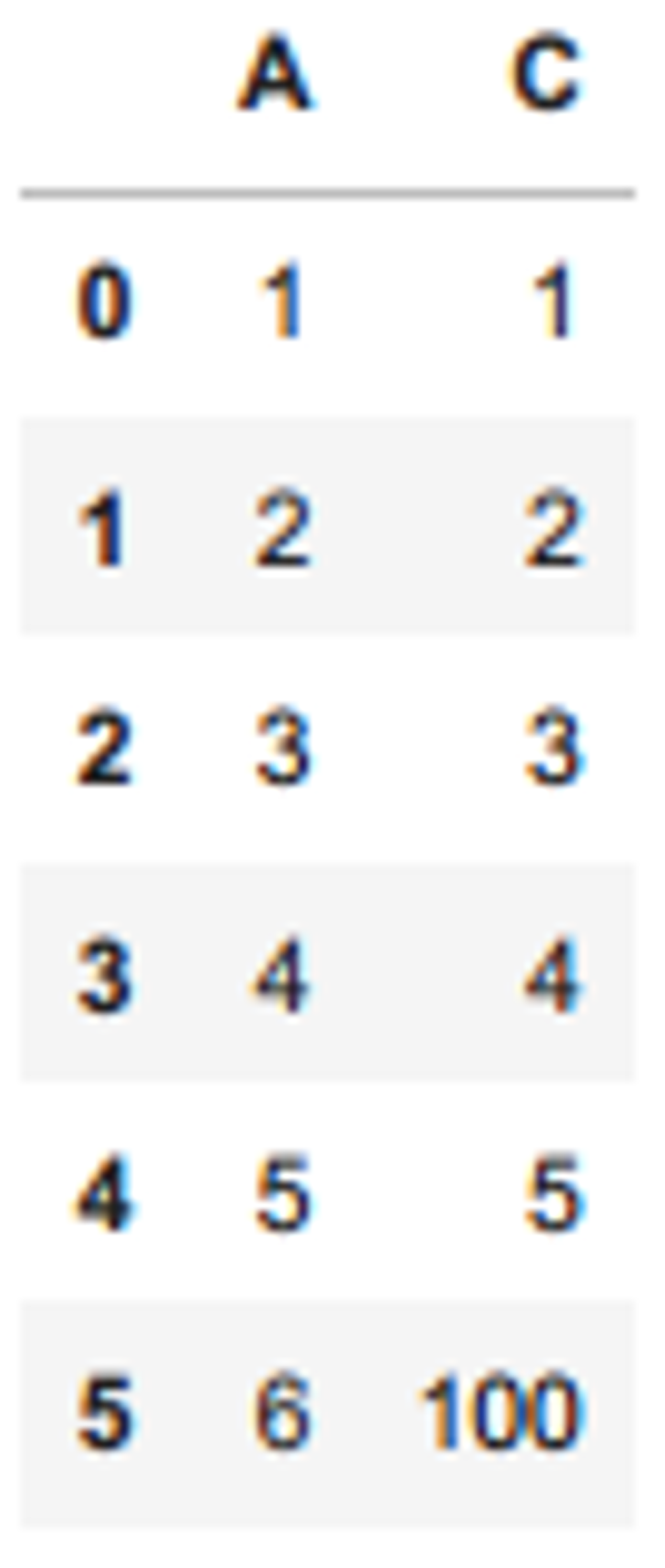
df.describe()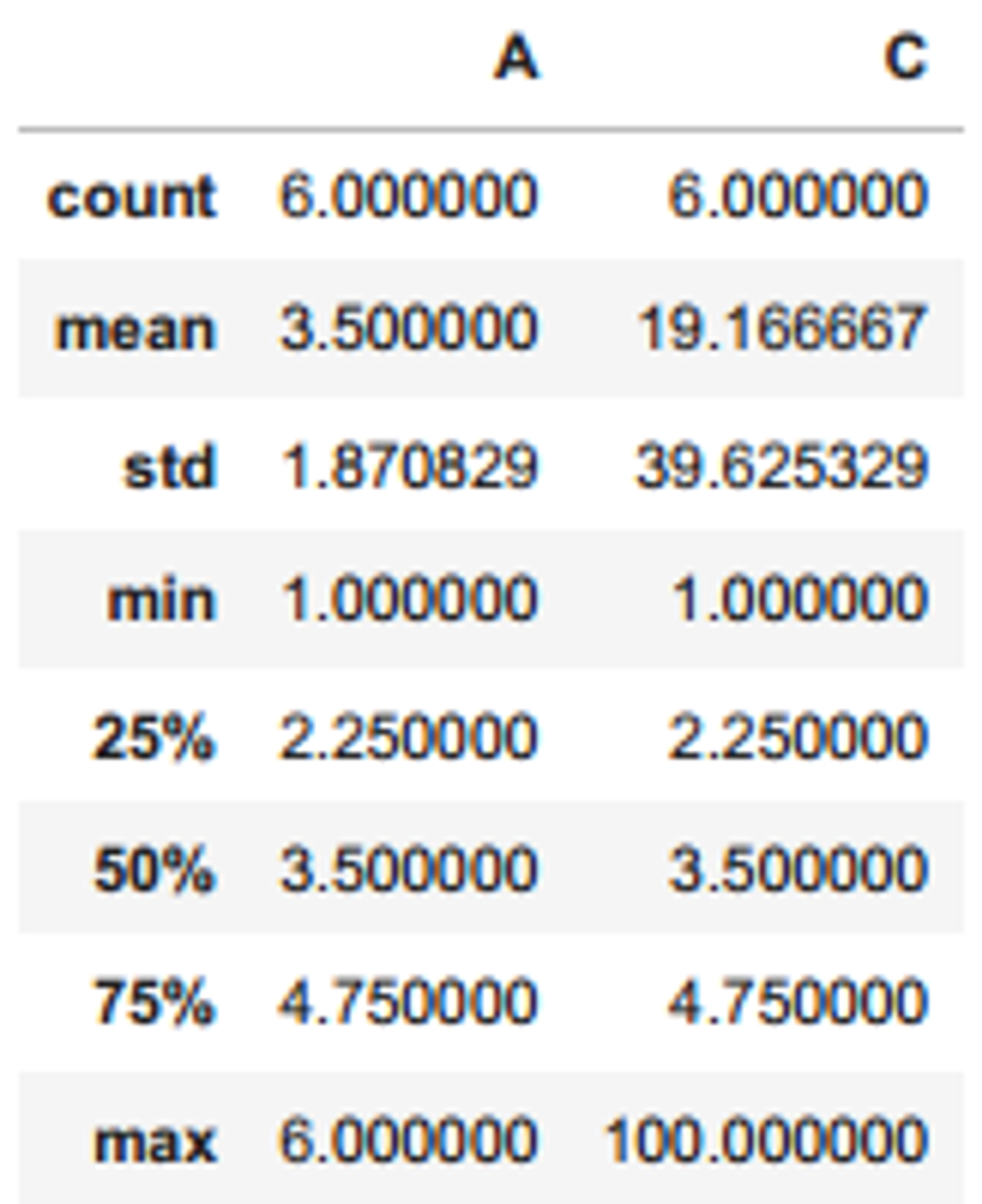
'빅데이터 분석가 양성과정 > Python' 카테고리의 다른 글
| 시각화 이용한 탐색적 데이터 분석(3) (0) | 2024.07.08 |
|---|---|
| 시각화 이용한 탐색적 데이터 분석(2) (1) | 2024.07.08 |
| plotly - 막대 그래프 / 세부 요소 변경 (0) | 2024.07.08 |
| plotly - 선 그래프 (0) | 2024.07.08 |
| plotly (0) | 2024.07.08 |
